Find the response of the system when the mass is subjected to the following initial conditions. 221 when the mass is subjected to the following initial conditions.
This is called a single degree of freedom RE Blake 2002.
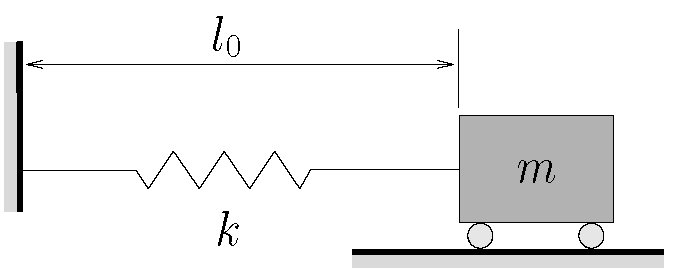
. Degree of freedom SDOF systems. The minimum number of indddependent coordinates required to determine completely the positions of all parts of a system at any instant of time defines the degree of freedom of the system. A single degree-of-freedom system comprises of m 10 kg f 20 N sm k 4000 N.
A system shown in Figure1 is a single-degree-of-freedom system since one coordinate x is sufficient to specify the position of the mass at any time. When a system in equilibrium under the influence of forces is given a virtual displacement. And the period T of oscillation in terms of natural frequency is _____.
Asingle degree of freedom systemrequires only one coordinate to describe its position at any instant of time. The cyclic frequency in terms of period T is _____. The horizontal vibrations of a single-story building can be conveniently modeled.
Free Vibration of an Undamped Translational System As the motion for the system in Figure1 is linear therefore we can use. Find the response of the system using Eq. Also find the time duration after which the system response will be fully a steady-state response.
A spring-mass system in horizontal position 2. If there is no external force applied on the system the system will experience free vibration. X_0 20 mm x_0 200 mms x_0 -20 mm x_0 200 mms x_0 20 mm x_0 -200 mms x_0 -20 mm x_0 -200 mms An undamped.
Single Degree of Freedom System- Free. Furthermore if there is no resistance or damping in the system the oscillatory motion will continue forever. Find total response of the system when an external force Ft 100 cos 10t is applied.
An undamped single-degree-of freedom system consists of a mass 5 kg and a spring of stiffness 2000 Nm. See Figure 3 M Ft ut Figure 2. Example of overhead water tank that can be modeled as SDOF system 1.
Single Degree of Freedom SDOF system m k Ft ut Figure 1. The differential equation of motion of mass m for the undamped system is. This chapter concerns the study of forced vibration of a single degree of freedom system treating undamped and damped system under harmonic periodic and arbitrary loading with different cases and examples.
The study of the free vibration of undamped and damped single-degree-of-freedom systems is fundamental to the understanding of more advanced. For an undamped system. The analysis and design of structures to resist the effect produced by time dependent forces or motions requires conceptual idealizations and simplifying assumptions through which the physical system is.
Single-Degree-of-Freedom Linear Oscillator SDOF For many dynamic systems the relationship between restoring force and deflection is approximately linear for small deviations about some reference. Mm тm a x 20 mm i 200 b x -20 mm š 200 sec sec тт тт c x 20 mm ž -200 d x -20 mm š -200 sec sec. Inertia force - which work to eliminate the acceleration of the mass.
In many practical systems the mass is distributed but for a simple analysis it can be approximated by a single point mass. Furthermore the mass is allowed to move in only one direction. The resonant frequency of a mass-spring system depends upon _____ a.
Undamped Single Degree-of-Freedom System. K spring stiffness m mass. Equation of Motion for the Single Degree of Freedom SDOF System.
Motion of the system will be established by an initial disturbance ie. The kinetic energy present in a single. Undamped single degree of freedom system.
Noureldin Ch3 Embarrassed by the Spirit Idleman Unplugged About my reference setups July 2021Intoduction to Undamped Free Vibration of SDOF 22 - Structural Dynamics Introduction to Undamped Free Vibration of SDOF 12 - Structural Dynamics Tutorial 3. An undamped single-degree-of-freedom system consists of a mass 5 kg and a spring of stiffness 2000 Nm. Free Vibration of Single-Degree- of- Freedom Systems Systems are said to undergo free vibration when they oscillate about their static equilibrium position when displaced from those positions and then released.
The total work done by the virtual forces 0 Displacement is imaginary infinitesimal instantaneous and compatible with the system When a virtual displacement dx is applied the sum of work done by the. Passing by all components of the general solution of an undamped forced system which are a transient solution depends only on initial conditions transient. If the system is complex eg a building that requires numerous variables to describe its properties it is possible.
21 Undamped single-degree-of freedom systems Example. The prototype single degree of freedom system is a spring-mass-damper system in which the spring has no damping or mass the mass has no stiffness or damping the damper has no stiffness or mass. Single-Degree-of-Freedom SDOF Systems Dynamic response of SDOF systems subjected to external loading Governing equation of motion mu cu ku Pt 1 the complete solution is u u homogeneous u particular u h u p 2 where u h is the homogeneous solution to the PDE or the free vi-bration response for Pt 0 and u.
In this chapter the governing equations of motion are formulated for free vibration of single-degree-of-freedom SDOF undamped system. Free undamped vibration single DoF Principle of virtual displacements. SINGLE DEGREE OF FREEDOM SYSTEM.
Undamped SDOF system its acceleration and opposing its motion. Free vibration of single-degree-of-freedom systems undamped in relation to structural dynamics during earthquakes. The angular natural frequency is given by.
Definition of an Undamped SDOF System. This force is constant with respect to frequency. None of the above.
𝑥 H0 Figure1. The natural frequency of an undamped single degree of freedom system is given by _____. Free Vibration kx mx kx mx kx mx x x F mx 2 2 2 0 Z Z Z Here there are two forces always acting on mass m namely Stiffness force - which work to bring the mass back to the position of equilibrium.
The frequencies at which they vibrate known as. Determine its natural frequency in terms of mass density of the liquid γ Buoyancy force - 0 n F gAx gA mx g Ax m γ γ γω. Vibration characteristics are studied by taking an example of a simple pendulum.
A cylidrical buoy of cross-sectional area A and total mass m is first depressed from equilibrium and then allowed to oscillate. Systems can be idealized as single-degree-of-freedom systems. The initial conditions are X 0 001 m x 0 0.
Equation of motion EOM Mathematical expression deflning the dynamic displacements of a structural sys-tem.
Undamped Single Degree Of Freedom System Springerlink

Engineering At Alberta Courses Undamped Single Degree Of Freedom System

0 Comments